- 칼만 필터를 사용할때는 state, 모델, Z 뭔지 반드시 설명 해야함
- 78.5hz 가 아쉽
- 최소 500hz 에서 law pass filter 한번 돌리고 다시 칼만을 넣으면 훨씬 더 정확해질 수 있음
- 연구 목적
IMU를 통해 받아들여지는 Raw Data를 KALMAN Filter를 사용하여 noise 제거 및 정확도 향상
- 연구 내용
IMU 센서는 자이로 센서, 가속도 센서, 지자기 센서로 구분 된다. IMU 센서는 Body Frame 에서의 값들을 측정한다. 자이로 센서는 각속도를 측정하는 센서이다. 각속도를 적분하는 방식으로 자세를 계산할 수 있다. 하지만 오차가 함께 계산이 된다는 단점이 있다. 가속도 센서는 센서 주변 외력에 의한 가속도를 측정하는 센서이다. 가속도 센서는 <그림2>와 같이 지구 중력을 계산함으로써 자세를 측정할 수 있다. 하지만 지구 중력 뿐만 아니라 Body 자체의 외력도 함께 계산 된다는 단점이 있다. 지자기 센서는 센서 주변의 자기장을 측정하는 센서 이다. <그림3>과 같이 지구의 자북을 계산하여 자세를 측정 할 수 있다. 하지만 지구 자기장뿐만 아니라 주변의 다른 자기장에도 영향을 많이 받는다는 단점이 있다.

그림 가속도 센서 자세 측정

그림 지자기 센서 자세 측정
정지상태일 때 자이로로 측정된 자세의 쿼터니언 x y z 값을 보면 <그림4>와 같다.



오차가 누적이 되어가는 모습을 볼 수 있다. 가속도와 지자기 센서로 측정한 자세 쿼터니언의 x y z 값은 <그림 5> 와 같다. 노이즈의 크기가 0.01 정도로 심하게 있는 것을 볼 수 있다. 오차의 누적과 노이즈로 IMU 의 Raw Data를 자세 측정에 그대로 쓰기는 어렵다.
그림 자이로로 측정한 자세 쿼터니언
그림 가속도와 지자기로 측정한 자세 쿼터니언
따라서 오차와 노이즈를 줄일 방안이 칼만 필터를 이용한 센서 융합이다.
칼만 필터는 상태 예측(state prediction)과 측정 업데이트(measurement update)를 반복적으로 수행하며 자세를 계산하는 과정이다. 칼만 필터의 단계를 나타내면 아래와 같다.
칼만 필터에서 측정값을 Z 예측값을 X 으로 사용된다. 칼만 필터에서는 칼만 Gain을 계산하게 되어 추정값 계산에서 측정값과 예측값의 비율을 결정하게 된다. 만일 칼만 Gain이 크다면 측정값이 큰 비율로 들어가게 되고, 칼만 Gain이 작다면 예측값이 큰 비율로 들어가게 된다.
칼만 필터를 사용할 때 쿼터니언을 기반으로 하였습니다. 오일러 각도로 하면 Gimbal Lock 문제가 발생 하므로 이를 방지 하기 위해 쿼터니언을 사용하였다.
초기 상태는 움직이지 않은 정지한 고정된 상태이기 때문에 값을 아래와 같이 설정하였다. 값은 실험에 의해 나왔던 표준편차 중에서 가장 큰 값을 기준으로 정하였다. 그리하여 는 단위행렬에 0.001을 곱한 값으로 설정하였다.
측정값인 Z는 이다. 따라서 H는 아래와 같다.


Q는 자이로로 계산된 쿼터니언의 표준편차의 제곱을 하였고 R은 가속도와 지자기 센서로 계산된 쿼터니언의 표준편차의 제곱으로 계산되었습니다. 값은 아래와 같다.


자세를
라고 한다면 아래와 같이 표현할 수 있다.
위의 식을 칼만 필터의 예측값 계산 과정에서 있는 식인 와 같은 형태로 변환하면 아래와 같다.
따라서


가 된다.
가속도 센서와 지자기 센서로 측정값인 Z를 계산하게 된다.
가속도 센서로 X 축과 Y 축 회전을 구할 수 있고, 지자기 센서로 Z 축 회전을 구하게 된다.
가속도 센서로 X 축과 Y 축의 회전을 구하는 식은 아래와 같다.

지자기 센서는 주변의 자기장에 영향을 많이 받는다.
따라서 지자기 센서 보정 과정을 거쳐야 한다. 지자기 센서의 주변 노이즈는 Hard Ironing과 Soft Ironing으로 분류할 수 있다. Hard Ironing을 2차원에서 표현하면 아래와 같다.
센서 주변에 부착된 일정한 자기장에 의하여 distortion이 발생 하게 된다. 그리하여 원의 중심과 센서의 위치와 차이가 나게 되는 것이다.
Soft Ironing을 2차원에서 표현하면 아래와 같다.
센서 주변의 일정하지 않은 자기장들에 의해 distortion이 발생 하게 된다. 그리하여 원으로 나와야 하는 주변의 자기장이 타원형으로 나오게 된다.
Hard Ironing과 Soft Ironing을 보정해주기 위해서는 지자기 센서의 각축에서 측정된 최댓값과 최솟값을 사용하여 보정할 수 있다. 식은 아래와 같다.

보정된 지자기 센서의 값을 사용하여 Z 축 회전을 구할 수 있다. 먼저 보정된 지자기 센서의 값에서 가속도 센서로 구해진 X축과 Y 축 회전의 역회전을 취한다. 역회전 된 값을 l이라 한다면 식은 아래와 같다.



따라서 Z 축의 회전을 쿼터니언으로 나타내면 아래와 같다.

칼만 필터를 사용하여 구한 자세 쿼터니언의 정확성을 알아보기 위해 모션 캡처 장비를 사용하여 다양한 상황에서 자세를 계산하였다. <그림8>, <그림10>과 같이 마커가 Rigid Body에 6개 부착되어 있습니다. <그림 7>, <그림9>와 같이 모션 캡처 카메라 4대가 Rigid Body의 마커들을 인식하여 자세 쿼터니언을 알 수 있다.



위와 같이 모션 캡처 장치를 설치하고 중앙에 IMU 센서를 위치시킨 후 실험을 진행하였다.
실험은
X 축 회전
Y 축 회전
Z 축 회전
원형 궤도와 Z 축 회전
y = x y = -x 축으로 회전
이렇게 5가지로 실험하여 모션 캡처와 비교 하였다. 또한 22분 30초 동안 가만히 있었을 때 값이 어떻게 나오는지 실험을 진행하였다.
실험의 오차를 구하는 방법은, 두 쿼터니언이 같다면 아래와 같이 나와야 한다.
하지만 두 쿼터니언이 다르다면
X Y Z 의 값에 0 이 아닌 값이 나오게 된다. (1-w), X, Y, Z의 값의 제곱 평균 제곱근(RMS)을 구하여 이를 오차로 측정하였다.

이렇게 구해진 의 크기를 q로 정의하였다. q의 값 비교를 통해 오차를 측정할 수 있다.

또한 칼만 필터로 구한 Roll, Pitch, Yaw와 모션 캡처로 구한 Roll, Pitch, Yaw 값의 차를 제곱 평균 제곱근(RMS)을 구하였다. 또한 움직이는 상황에서 칼만 필터로 구현된 자세 쿼터니언 값이 모션 캡처로 구현된 값보다 어느 정도 느리게 값이 나오는지 측정하였다.
- X 축으로 회전한 결과


위의 3축이 모션 캡처로 구한 자세 쿼터니언이고, 아래 3축이 칼만 필터로 구한 자세 쿼터니언 이다.
X 축으로 회전할 때 자세 쿼터니언의 x값을 그래프로 표현하면 아래와 같다.

쿼터니언의 오차를 그래프로 그리면 아래와 같다.


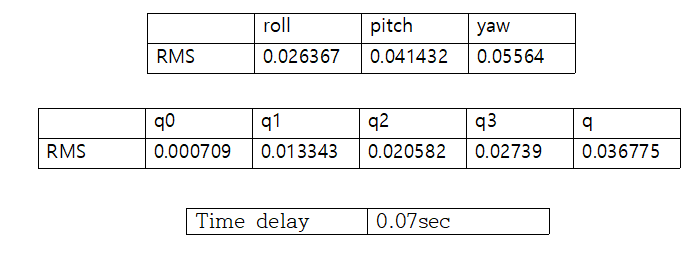
오차 roll, pitch, yaw, q0, q1, q2, q3, q 값의 RMS를 구하면 아래와 같다.
- Y 축으로 회전한 결과


위의 3축이 모션 캡처로 구한 자세 쿼터니언이고, 아래 3축이 칼만 필터로 구한 자세 쿼터니언 이다.
Y 축으로 회전한 자세 쿼터니언의 Y값을 그래프로 그리면 아래와 같다.

쿼터니언의 오차를 그래프로 그리면 아래와 같다.


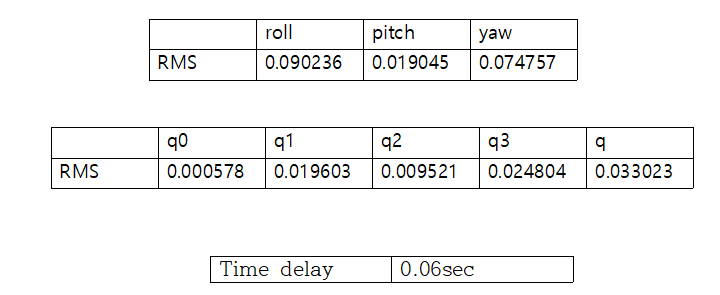
오차 roll, pitch, yaw, q0, q1, q2, q3, q 값의 RMS를 구하면 아래와 같다.
- Z 축으로 회전한 결과


위의 3축이 모션 캡처로 구한 자세 쿼터니언이고, 아래 3축이 칼만 필터로 구한 자세 쿼터니언 이다.
Z 축으로 회전한 자세 쿼터니언의 Z값을 그래프로 그리면 아래와 같다.


쿼터니언의 오차를 그래프로 그리면 아래와 같다.

오차 roll, pitch, yaw, q0, q1, q2, q3, q 값의 RMS를 구하면 아래와 같다.
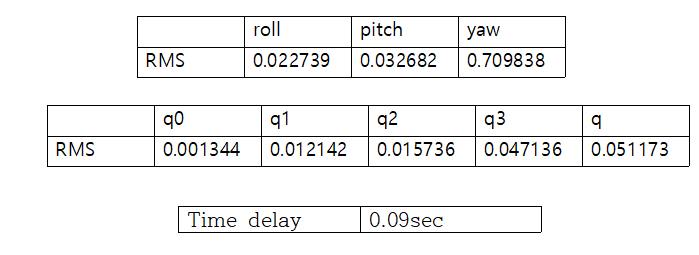
- 원형 궤도이동 및 Z 축 회전 결과


위의 3축이 모션 캡처로 구한 자세 쿼터니언이고, 아래 3축이 칼만 필터로 구한 자세 쿼터니언 이다.
원형 궤도 회전 및 Z 축으로 회전한 자세 쿼터니언의 X, Y, Z값을 그래프로 그리면 아래와 같다.

쿼터니언의 오차를 그래프로 그리면 아래와 같다.


오차 roll, pitch, yaw, q0, q1, q2, q3, q 값의 RMS를 구하면 아래와 같다.

- y = x, y = -x 축으로 회전하였을 때 결과
Y = -x 축 회전 상태 일 때

Y = x 축 회전 상태 일 때

위의 3축이 모션 캡처로 구한 자세 쿼터니언이고, 아래 3축이 칼만 필터로 구한 자세 쿼터니언 이다.
y = x 축과 y = -x 축으로 회전하였을 때 쿼터니언의 X, Y, Z값을 그래프로 나타내면 아래와 같다.





쿼터니언의 오차를 그래프로 그리면 아래와 같다.


오차 roll, pitch, yaw, q0, q1, q2, q3, q 값의 RMS를 구하면 아래와 같다.
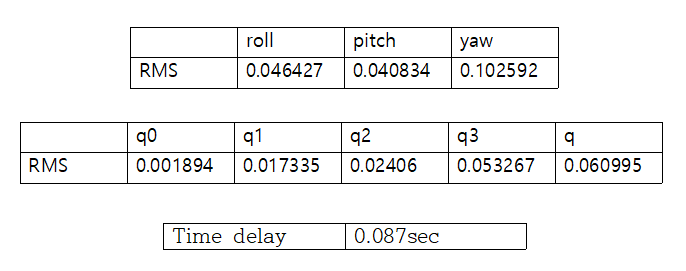
- 22분 30초 동안 정지 상태일 때
모션 캡처와 칼만 필터를 함께 측정하였던 실험장소가 아닌 다른 장소에서 지자기 보정을 한 뒤, 정지 상태에서 측정해 보았다.
22분 30초 동안의 측정된 자세 쿼터니언을 그래프로 나타내면 아래와 같다.


오차 roll, pitch, yaw, q0, q1, q2, q3, q 값의 RMS를 구하면 아래와 같다.

- 상보 필터와 비교
상보 필터로 계산된 X 축 회전, Y 축 회전, Z 축 회전, 원형 궤도 이동 및 Z 축 회전, y = x 와 y = -x 축 회전의 오차와 칼만 필터로 계산된 오차는 아래와 같다.
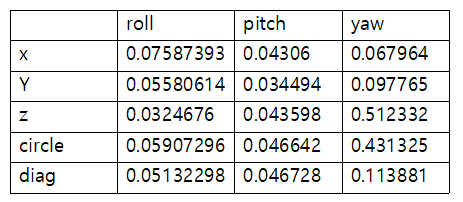

칼만 필터로 계산된 오차는 아래와 같다.

칼만 필터로 구현한 자세 쿼터니언이 상보 필터로 구현한 자세 쿼터니언에 비해서 성능이 평균 약 37% 정도 더 정확하였다.
- 연구 성과
기존의 IMU에서 Raw Data를 이용하여 값을 계산하면 노이즈가 심하고, 시간이 지나면 오차가 누적되며 자신의 가속도도 오차가 되는 여러 단점이 있었다. 이를 보완하기 위하여 노이즈 감소와 정확한 값을 추정할 수 있는 칼만 필터를 만들고 적용하였다. 다양한 자세에서 다양한 움직임에서 적용할 수 있게 되었으므로 활용도가 높으리라 생각한다.
- REFERENCE
- VALENTI, Roberto G.; DRYANOVSKI, Ivan; XIAO, Jizhong. Keeping a good attitude: A quaternion-based orientation filter for IMUs and MARGs. Sensors, 2015, 15.8: 19302-19330.
- MARKLEY, F. Landis. Attitude error representations for Kalman filtering. Journal of guidance, control, and dynamics, 2003, 26.2: 311-317.
- Code
'Sensor fusion' 카테고리의 다른 글
| Extended Kalman Filter & Error state Kalman Filter (IMU + Motion Capture) (6) | 2020.07.23 |
|---|---|
| imu 센서를 활용한 attitude estimation (quaternion base) (4) | 2020.02.10 |
| Kalman Filter (2) | 2020.01.11 |


